 |
| Girolamo Cardano (1501 - 1576) |
Números Complexos
- I: Introdução, Definições e Operações Simples
- II: Propriedades e Operações Avançadas
Um pouco de história...
Até o século XVI, era considerada absurda a existência de raízes quadradas negativas. Portanto, equações como x² + 4 = 0 não possuíam solução segundo os matemáticos da época. O matemático Girolamo Cardano mostrou que mesmo uma equação tendo em uma de suas raízes uma raiz quadrada negativa, era possível que esta fosse uma solução da equação.
Especificamente, Cardano resolveu o seguinte problema, publicado em seu livro Ars Magna: "Encontre dois números cuja soma seja 10 e o produto seja 40".
Como curiosidade, é importante citar que Cardano não realizou isso sozinho - ele roubou o método para resolver esse tipo de problema do matemático Tartaglia, ao qual havia prometido não divulgar seu método.
Definição
Convencionou-se que a letra i representaria a unidade imaginária, que é a raiz quadrada de -1.
Define-se número complexo como qualquer número que possa ser representado na forma z = a + bi, onde a e b são coeficientes reais, sendo a chamado de parte real (representada por Re(z)) e b a parte imaginária (representada por Im(z)) de z. Portanto, a conclusão imediata é que todo número real é complexo, já que b pode ser zero.
Números complexos no plano e algumas definições importantes
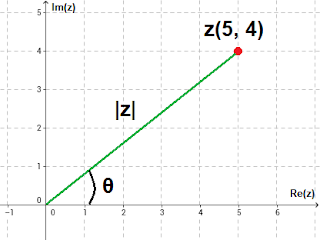
A representação de complexos num plano bidimensional ocorre através do plano Argand-Gauss, em que o eixo x representa a parte real do número complexo e o eixo y, a parte imaginária. A seguir, um exemplo:
Um ponto no plano representa o número complexo. O do exemplo (ponto vermelho), temos o complexo z = 5 + 4i. O ângulo θ é chamado de argumento de z ou, simplesmente, arg(z). A distância entre a origem do sistema de coordenadas e o número complexo (representada pelo segmento verde) é definida como módulo de z ( |z| ).
Uma outra definição importante é o conjugado de um número complexo. O conjugado de um número complexo z = a + bi é z' = a - bi. O conjugado é representado por uma barra vertical ( ¯ ) sobre o complexo. Por conformidade, representaremos o conjugado por z'.
Outras formas de representação de um complexo
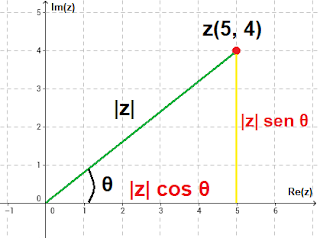
Considere o triângulo do plano anterior:
Fazendo Pitágoras no triângulo:
|z|² = [Re(z)]² + [Im(z)]²
No caso apresentado, Re(z) = 5 e Im(z) = 4. Guarde este resultado importante!
Note também que Re(z) = |z| * cos θ e que Im(z) = |z| * sen θ. Então, podemos representar z assim:
z = Re(z) + Im(z) * i
z = |z| (cos θ + i * sen θ) ou z = |z| * cis θ
Esta forma é chamada de forma trigonométrica de um número complexo. Considere que cis θ = cos θ + i * sen θ.
Há também a forma exponencial do complexo, cuja demonstração não convém a nível de ensino médio:
z=|z|×eiθ
Em que e representa o número de Euler. Note que:
cosθ+isenθ=cisθ=eiθ
Potências da unidade imaginária
Temos as seguintes potências básicas: (cuja demonstração é imediata)
Perceba que essas quatro potências fecham um ciclo, já que i elevado a 4 é 1, i elevado a 5 é i... Portanto, um método para determinar o valor para expoentes maiores é dividir o expoente por quatro: O quociente é a quantidade de "ciclos", e o resto é exatamente o expoente simplificado. Portanto, para i elevado a 82ª potência, temos 2 como resto de divisão do expoente e, portanto, o valor da potência é igual a -1.
Soma
Sejam dois complexos z = a + bi e w = c + di. A soma deles é dada por:
z + w = (a + c) + (b + d)i
Portanto, só se soma parte real com parte real e parte imaginária com parte imaginária! A subtração é imediata:
z - w = (a - c) + (b - d)i
Multiplicação
A multiplicação é feita normalmente através da propriedade distributiva:
z * w = (a + bi)(c + di)
z * w = ac + adi + bci - bd
z * w = (ac - bd) + (ad + bc)i
Lembrando que i² = -1, e por isso bi * di = -bd.
Divisão
A divisão é um pouco mais complicada: elimine o termo imaginário do denominador multiplicando numerador e denominador (lembre-se de que você pode fazer isso!) por outro complexo que elimine esse termo. Veja um exemplo:
z = 8 + 4i
w = 5 + 3i
Perceba que foi usado um produto notável: a diferença de dois quadrados. Essa técnica pode ser usada sempre que se deseja eliminar a parte imaginária de um complexo, já que i² = -1. No módulo seguinte, explicamos melhor porque isso acontece.
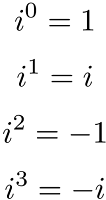









Nenhum comentário:
Postar um comentário